Radiology Universe Institute
Lost SoulsLost Souls Pediatric AtlasPeds Atlas Ellipsoid Volume CalculatorVolumes Aortic DiameterAortic Diameter - Adult Kidney SizeKidney Size - Peds Spleen SizeSpleen Size - Peds Testicular VolumeTesticular Volume Fleishner Society Lung Nodule Follow-up Recommendations for Solid, Subsolid, and Groundglass Lung Nodules 2017Lung Nodule 2017 ContactContact

Pediatric Kidney Size Percentile Calculator

contributed by Michal Kulon, MD on 9/15/2015
Year Month Day
Date of Scan:
Date of Birth:
Right Kidney: cm
Left Kidney: cm
For age of 0 years 0 months 0 days, the average kidney length is 4.43 cm and standard deviation is 0.29 cm.
Right kidney length of 0 cm corresponds to 0 percentile (15.35 standard deviations below the mean).
Left kidney length of 0 cm corresponds to 0 percentile (15.35 standard deviations below the mean).




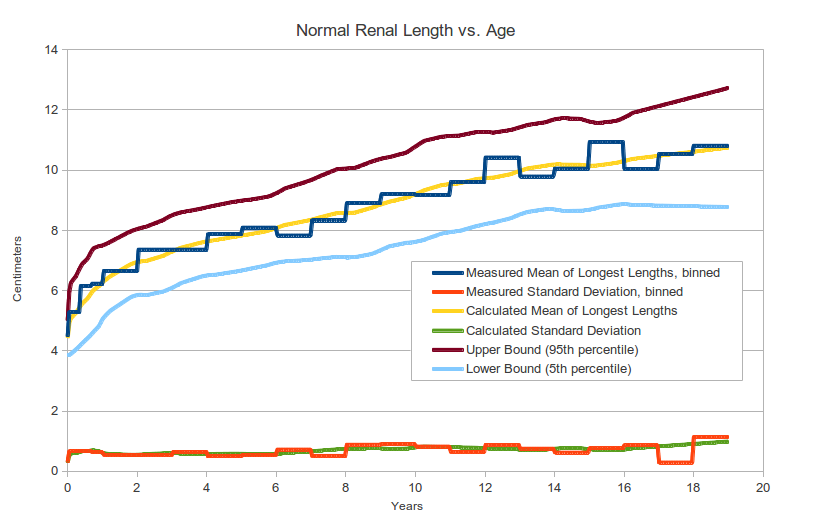
Normal Renal Length ranges in children vs. age, based on pediatric kidney ultrasound

Methods

  • Normal range data based on "Sonographic Assessment of Renal Length in Normal Children" AJR 142:467-469, March 1984
  • Source data consists of 203 patients under 19 years old. However, this population is divided into numerous age intervals, with each interval containing relatively few patients (4 to 54). This yields good overall regression, but relatively poor statistical quality within some of the individual age intervals, leading to several spurious results such as the mean kidney size within the 15-16 year old group being apparently larger than for the older ages of 16-17 year old.
  • This calculator smooths out the spurious results by performing multiple linear regressions, each linear regression centered at the age of interest, spanning relatively short age range. Exceptions are made for youngest and oldest age groups, where it not possible to center the linear regression, and also for ages under 3 years old, where linear regression over several years is not appropriate due to the curvature of the data for this age range. In calculating regression, higher weight is given to the age inteval containing more patients.
    • Ages 0 to 1 month: linear regression spans age 0 to 1 month.
    • Ages 1 month to 3 years old: linear regression spans +/- 1 age intervals.
    • Ages 3 to 17: linear regression spans 5 year interval centered at the 1-year age interval of interest (i.e. +/- 2 age intervals).
    • Ages 17 to 19: linear regression spans 4 year interval 15 to 19 years old.
  • Calculation of percentiles assumes non-skewed, approximately normal distribution, and that the mean approximately equals the median.

Additional Resources